读完《剑指offer》之后发现有一些算法题有点不理解,故在此记录一下解题思路和代码
1.矩阵中的路径
请设计一函数,用来判断再一个矩阵中是否存在一条包含某个字符串所有字符的路径。路径可以从矩阵中的任意一格开始,没异步可以再矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子
这个问题可以使用回溯法来解决,即先找到待匹配字符串的第一个字符,然后再从上下左右分别确认第二个字符是否相同,依次类推。如果发现已经匹配到第n个字符,从它的上下左右匹配第n+1个字符的时候发现无法匹配,那么就回退到已匹配第n-1个字符的点继续匹配。
回溯法三部曲:
1
2
3
4
5
6
7
8
9
10
11
12
| void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (从本层集合中遍历元素) {
处理选择的元素节点;
backtracking(路径, 选择下一层列表);
回溯,撤销处理结果;
}
}
|
回溯法能解决的问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多要符合条件的子集
- 棋盘问题:N皇后,解数独等等
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| class Solution {
public:
bool exist(vector<vector<char>>& board, string word) {
// 假定矩阵大小最大为6*6
bool visited[6*6] = {0};
memset(visited, 0 , 6 * 6 * sizeof(bool));
for (int i = 0; i < board.size(); ++i) {
for (int j = 0; j < board[0].size(); ++j) {
if (hasPath(board, word.c_str(), visited, i, j)) {
return true;
}
}
}
return false;
}
bool hasPath(vector<vector<char>> &board, const char *str, bool *visited, int row, int col) {
if (*str == '\0')
return true;
const int cols = board[0].size();
if (col < 0 || col >= cols) {
return false;
}
if (row < 0 || row >= board.size()) {
return false;
}
if (visited[cols * row + col] || board[row][col] != *str) {
return false;
}
str++;
visited[cols * row + col] = true;
// left right top bottom
bool has = hasPath(board, str, visited, row, col - 1)
|| hasPath(board, str, visited, row, col + 1)
|| hasPath(board, str, visited, row - 1, col)
|| hasPath(board, str, visited, row + 1, col);
if (!has) {
// back to last
visited[cols * row + col] = false;
str--;
}
return has;
}
};
|
2. 1~n 整数中1出现的次数
输入一个整数n, 求1 ~ n这n个整数的十进制表示中1出现的次数.例如,输入12, 1 ~ 12这些整数中包含1的数字有 1,10,11和12,1一共出现5次
可以分开看,即1出现在每一位上的次数.例如n是一个3位数,那么1出现的次数就是1出现在个位上的次数加上1出现在十位上的次数再加上1出现再百位上的次数.
例如1 ~ 3012:
如果个位固定为1, 高位就可以在[0, 301]这个范围内取值即1 ~ 3011共302个1(高位的1先不计算,只计算个位出现的1), 那么就是301 + 1
十位固定为1的话,高位就可以在[0, 29]这个范围内取值即10 ~ 2919共30*10个1, 然后还剩余3010,3011,3012三个数共3个1
百位固定为1的话,高位就可以在[0, 2]这个范围取值即100 ~ 1199共3*100个1
所以规律总结起来就是:
当前位的值=0, 那么1出现的次数为 (high + 1) * rank
当前位的值=1, 那么1在当前位出现的次数为 high * rank + low + 1
当前位的值>1, 那么1在当前位出现的次数为 high * rank + 1
high为当前位之前的数字, rank为当前位的数量级(个位为1,十位为10,百位为100,依次类推), low为当前位之后的数字
实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| int count_times_other(int num)
{
int cnt = 0;
int base = 1; // 当前位的数量级
while (base <= num)
{
int low = num % base;
int cur = (num / base) % 10;
int high = num / (base * 10);
if (cur == 0) {
cnt += high * base;
}
else if (cur == 1) {
cnt += high * base + low + 1;
}
else {
cnt += (high + 1) * base;
}
base *= 10;
}
return cnt;
}
|
3. 把数字翻译成字符串
给定一个数字,我们按照如下规则把它翻译成字符串:0-a, 1-b … 25-z。一个数字可能有多个翻译,例如12258有5中不同的翻译,分别是bccfi, bwfi,bczi,mcfi,mzi。请编程实现一个函数,用来计算一个数字有多少种不同的翻译
这题和青蛙跳类似,一次可以取一位数字,也可以取两位数字,只是取两位数字需要满足一定的条件。
如果第i位和第i-1位数字组合起来落在[10, 25]这个区间那么,那么第i位的翻译需要分两种情况来讨论,即单独翻译第i位数字或者将第i位和第i-1位组合起来翻译。定义f(i)为i位长度的数字总共的翻译方法数量,那么f(i) = f(i - 1) + f(i - 2)
如果第i位和第i-1位数字组合起来没有落在[10, 25]这个区间,那么第i位只能单独翻译了,那么f(i) = f(i - 1)
代码实现有两种方式:
方式1:将数字转换成字符串,方便取值计算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| int translate_number_count(int num)
{
int first = 1, second = 1, cnt = 0;
char [16] = {0};
int len = snprintf(str, sizeof(str) - 1, "%d", num);
for (int i = 2; i < len; ++i) {
int n = str[i - 1] - '0';
n += (str[i - 2] - '0') * 10;
if (n >= 10 && n <= 25) {
first = first + second; // 当前长度的统计数量, f(i) = f(i-1) + f(i-2)
second = first - second; // 上一个长度的统计数量, f(i-1) = f(i) - f(i - 2)
}
else {
second = first; // 只有一种翻译方式,所以不变, f(i-1) = f(i)
}
}
return first; // f(i)
}
|
方式2:直接使用数字
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| int translate_number_count_other(int num)
{
int first = 1, second = 1;
int one = num % 10; // 个位数字
int two = 0; // 十位数字
while (num != 0)
{
num /= 10;
two = num % 10;
int tmp = two * 10 + one;
if (tmp >= 10 && tmp <= 25) {
first = first + second; // f(i) = f(i-1) ++ f(i-2)
second = first - second; // f(i - 1) = f(i) - f(i-2)
}
else {
second = first; // f(i-1) = f(i)
}
one = two;
}
return first;
}
|
复杂度计算:
第一种实现方式中因为只和数字的十进制位数有关,所以时间复杂度位O(logN), 动态申请的字符串也是和数字长度有关,所以空间复杂度为O(logN).
第二种实现方式和第一种方式一样,所以时间复杂度为O(logN), 但是空间复杂度为O(1)
4. 数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数
暴力的方法就是依次扫描每个数字,然后与其后面的数字比较大小。这样的时间复杂度是O(N^2).
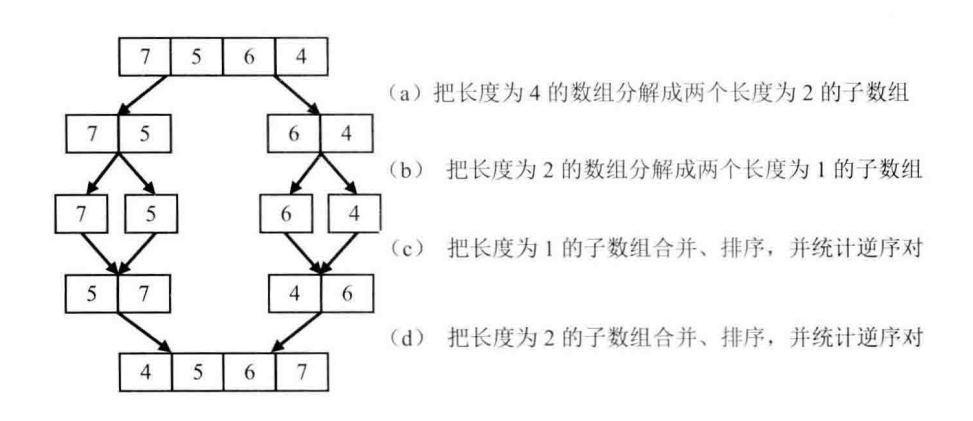
更简单的方法应该是比较相邻的数字,然后确定逆序对的数量。使用归并排序的思想来进行比较相邻的数字,这样就能比较快的统计出逆序对的总数,归并排序的复杂度是O(NlogN)

代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| int inverse_pairs_core(int *data, int *copy, int start, int end)
{
if (end <= start) {
copy[start] = data[start];
return 0;
}
int count = 0;
int mid = (start + end) / 2;
count += inverse_pairs_core(copy, data, start, mid);
count += inverse_pairs_core(copy, data, mid + 1, end);
int left = mid;
int right = end;
int index = end;
while (left >= start && right >= (mid + 1)) {
if (data[left] >= data[right]) {
count += right - mid; // 右边当前元素之前的全部比左边当前元素小
copy[index--] = data[left--];
}
else {
copy[index--] = data[right--];
}
}
// 复制左边剩余元素,右边所有元素都比左边的大,所以左边剩余的元素都比右边的小
while (left >= start) {
copy[index--] = data[left--];
}
// 复制右边元素,左边元素都比右边的大
while (right >= (mid + 1)) {
// 已经计算过一次了,不用重复计算, 直接拷贝
copy[index--] = data[right--];
}
return count;
}
int inverse_pairs(int *data, int length)
{
if (!data || length <= 1)
return 0;
int *copy = new (std::nothrow) int[length];
if (!copy)
return -1;
memcpy(copy, data, length * sizeof(int));
return inverse_pairs_core(data, copy, 0, length - 1);
}
|
归并排序的时间复杂度为O(NlogN), 这里使用到了一个辅助数组,所以空间复杂度为O(N)
5. 队列的最大值
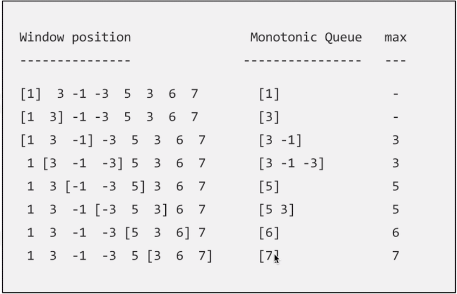
给定一个数组的滑动窗口的大小,请找出所有滑动窗口历的最大值。例如,输出数组{2,3,4,2,6,2,5,1},以及滑动窗口大小3, 它们的最大值分别为{4,4,6,6,6,5}
常规方法的话就是遍历数组,然后根据窗口大小找到当前窗口中的最大值,其时间复杂度为O(NK), k为窗口大小。还有一种改良方法就是,滑动的时候如果最大值没有滑出当前窗口那么就无需再重新遍历当前窗口了,否则的话就需要遍历当前窗口,其平均时间复杂度优于前一种方式。
还一种方式就是使用双向队列记录滑动窗口中的最大值,队列的头为窗口中的最值,其他为次大值。如果将要滑入窗口的数比当前窗口中的最大值大那么就将该值放入队列头部;如果小,那么将队列中比它小的数全部删除。

实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| vector<int> window_max_value(const vector<int> &data, int window)
{
if (data.empty() || window < 1 || data.size() < window)
return vector<int>();
// 最大值队列, 只保存下标值
deque<int> index;
// 先将 窗口大小的数据入列
for (int i = 0; i < window; ++i) {
while (!index.empty() && data[i] >= data[index.back()]) {
index.pop_back(); //将队尾其他小的值从队列中删除
}
index.push_back(i); // 将最大值放入队列或者将比当前小的值放入队尾
}
vector<int> ret; // 返回结果
ret.push_back(data[index.front()]);
for (int i = window; i < data.size(); ++i) {
if (i - index.front() >= window) {
index.pop_front();
}
while (!index.empty() && data[i] >= data[index.back()]) {
index.pop_back(); //将队尾其他小的值从队列中删除
}
index.push_back(i);
ret.push_back(data[index.front()]);
}
return ret;
}
|
6. n个骰子的点数
把n个骰子扔再地上,所有骰子朝上的点数之和为s。 输入n, 打印出s的所有可能的出现的概率
题目需要我们求出所有点数出现的概率,根据概率出现的计算公式,点数 k 出现概率计算公式为:
P(k)= k出现次数 / 总次数
投掷 n 个骰子,所有点数出现的总次数是 6^n,因为一共有 n 枚骰子,每枚骰子的点数都有 6 种可能出现的情况。我们的目的就是 计算出投掷完 n 枚骰子后每个点数出现的次数。
使用递归造成重复计算的问题
单纯使用递归搜索解空间的时间复杂度为 6^n,会造成超时错误,因为存在重复子结构。解释如下:
我们使用递归函数 getCount (n,k) 来表示投掷 n 枚骰子,点数 k 出现的次数。
为了简化分析,我们以投掷 2 枚骰子为例。
我们来模拟计算点数 4 和点数 6,这两种点数各自出现的次数。也就是计算 getCOunt (2,4) 和 getCount (2,6)。
他们的计算公式为:
getCount(2,4) = getCount(1,1) + getCount(1,2) + getCount(1,3)
getCount(2,6) = getCount(1,1) + getCount(1,2) + getCount(1,3) + getCount(1,4) + getCount(1,5)
我们发现递归统计这两种点数的出现次数时,重复计算了 getCount(1,1) + getCount(1,2) + getCount(1,3)
这些子结构,计算其它点数的次数时同样存在大量的重复计算。
参考链接
动态规划
动态规划解决问题一般分为三步:
1.表示状态
2.找出状态转移方程,即递推关系式
3.边界处理
表示状态
分析问题的状态时,不要分析整体,只分析最后一个阶段即可!因为动态规划问题都是划分为多个阶段的,各个阶段的状态表示都是一样,而我们的最终答案就是在最后一个阶段。
对于这道题,最后一个阶段是什么呢?
通过题目我们知道一共投掷 n 枚骰子,那最后一个阶段很显然就是:当投掷完 n 枚骰子后,各个点数出现的次数。
注意:这里的点数指的是前 n 枚骰子的点数和,而不是第 n 枚骰子的点数,下文同理。
找出了最后一个阶段,那状态表示就简单了。
首先用数组的第一维来表示阶段,也就是投掷完了几枚骰子。
然后用第二维来表示投掷完这些骰子后,可能出现的点数。
数组的值就表示,该阶段各个点数出现的次数。
所以状态表示就是这样的 dp [i][j],表示投掷完 i 枚骰子后,点数 j 的出现次数。
找出状态转移方程
找状态转移方程也就是找各个阶段之间的转化关系,同样我们还是只需分析最后一个阶段,分析它的状态是如何做到的。
最后一个阶段也就是投掷完 n 枚骰子后的这个阶段,我们用 dp [n][j] 来表示最后一个阶段点数 j 出现的次数。
单单看第 n 枚骰子,它的点数可能为 1,2,3,4,5,6,因为投掷完 n 枚骰子后点数 j 出现的次数,可以由投掷完 n-1 枚骰子后,对应点数 j-1,j-2,j-3,j-4,j-5,j-6 出现的次数转化过来。
1
2
3
| for (第n枚骰子的点数 i = 1; i <= 6; i ++) {
dp[n][j] += dp[n-1][j - i]
}
|
写成数学公式是这样的:
1
2
3
| 6
dp[n][j]= ∑ dp[n−1][j−i]
i=1
|
n 表示阶段,j 表示投掷完 n 枚骰子后的点数和,i 表示第 n 枚骰子会出现的六个点数。
边界处理
这里的边界处理很简单,只要我们把可以直接知道的状态初始化就好了。
我们可以直接指导的状态是啥,就是第一阶段的状态:投掷完 1 枚骰子后,它的可能点数分别为 1,2,3,4,5,6,并且每个点数出现的次数都是 1.
1
2
3
| for (int i = 1; i <= 6; i ++) {
dp[1][i] = 1;
}
|
代码实现为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| // 求出n个骰子所有点数和的概率
void print_probability(const int num)
{
if (num < 1)
return;
// int[i][j], i为骰子个数,j为i个骰子点数和为j出现的次数
// max(i) = num + 1, max(j) = (num + 1) * 6
const int maxi = num + 1;
const int maxj = (num + 1) * 6;
int *dp = (int *)malloc(maxj * maxi * sizeof(int));
if (!dp) return;
memset(dp, 0, maxj * maxi * sizeof(int));
// 初始状态, 1个骰子
for (int i = 1; i <= 6; i++) {
*(dp + 1*maxj + i) = 1; // dp[1][i] = 1;
}
for (int i = 2; i <= num; i++) {
for (int j = i; j <= 6 * i; j++) {
for (int x = 1; x <= 6; x++) {
if (j - x <= 0) {
break; // 单个点数还没总点数多,所以后面的就不用计算了
}
// dp[i][j] += dp[i - 1][j - x];
*(dp + (i * maxj) + j) += *(dp + ((i - 1) * maxj) + j - x);
}
}
}
int total = pow(6, num); // 所有点数出现的总次数,[num, 6*num]
// 计算概率
for (int j = num; j <= 6 * num; j++) {
int cnt = *(dp + num * maxj + j); // dp[num][j]
printf("P(%d)=%f ", j, cnt * 1.0 / total);
}
printf("\n");
free(dp);
}
|
其实上述实现还可以进一步优化,从递推关系式dp[i][j] += dp[i - 1][j - x]可以知道,i个骰子的点数和只和i-1个骰子的点数和有关,所以没有必要保存所有的骰子的点数和,只需要保存本次和上一轮的骰子点数和即可。