KMP算法中的DFA计算

假定模式字符串为 “ABABAC”
1. 构造DFA
推入第一位字符
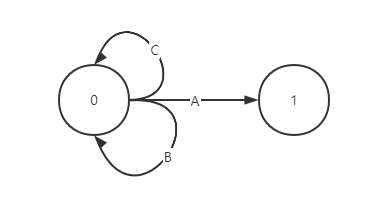
当推入的字符是A时匹配,往下走一步即 1; 当推入B或C时不匹配,那就还在原地呆着即 0
推入第二位字符
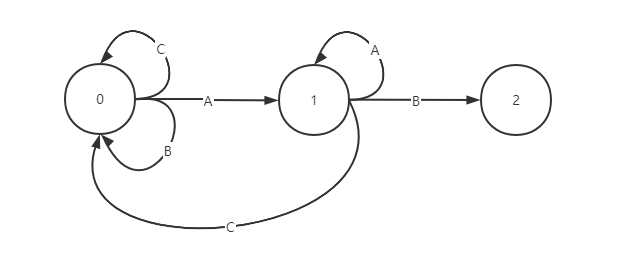
当推入B时匹配,行进到下一步即 2 当推入字符A时不匹配,掐头将剩下的字串 A 推入自动机,行进到 1 当推入字符C时不匹配,掐头将剩下的字串 C 推入自动机,行进到 0
推入第三位字符
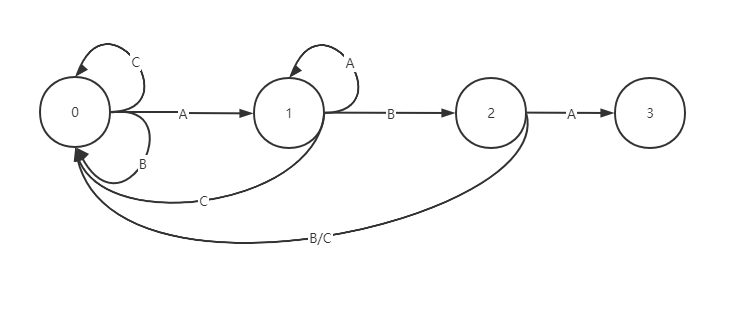
当推入的是A时匹配,往下一步走即 3; 当推入字符B或C时不匹配,掐头将剩下的字符BB或BC依次推入自动机,都是只能进行到 0
推入第四位字符
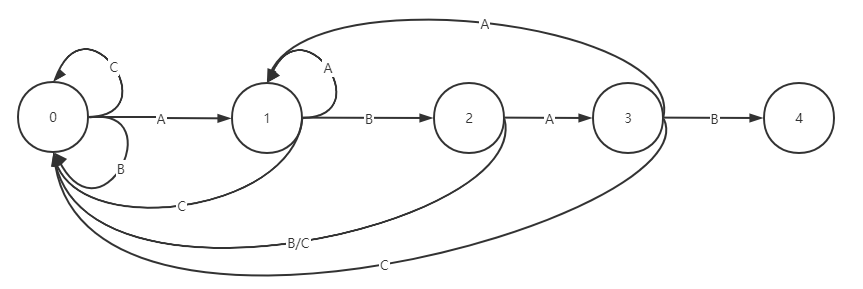
当推入的是字符B时匹配,行进到下一步 4; 当推入字符A时不匹配,掐头将剩下的字串BAA依次推入自动机会行进到 1; 当推入字符C时不匹配,掐头将剩下的字串BAC依次推入自动机会行进到 0
推入第五位字符
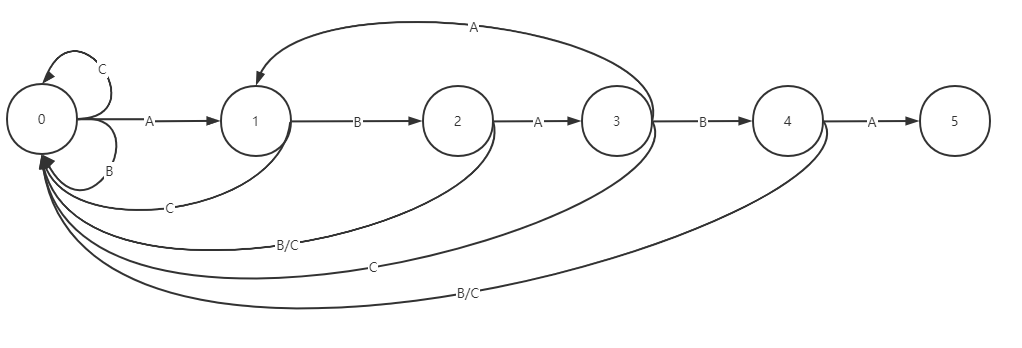
当推入字符A时匹配,行进到下一步 5; 当推入字符B时不匹配,掐头将剩下的字串BABB推入自动机会行进到 0; 当推入字符C时不匹配,掐头将剩下的字串BABC推入自动机会行进到 0
推入第六位字符
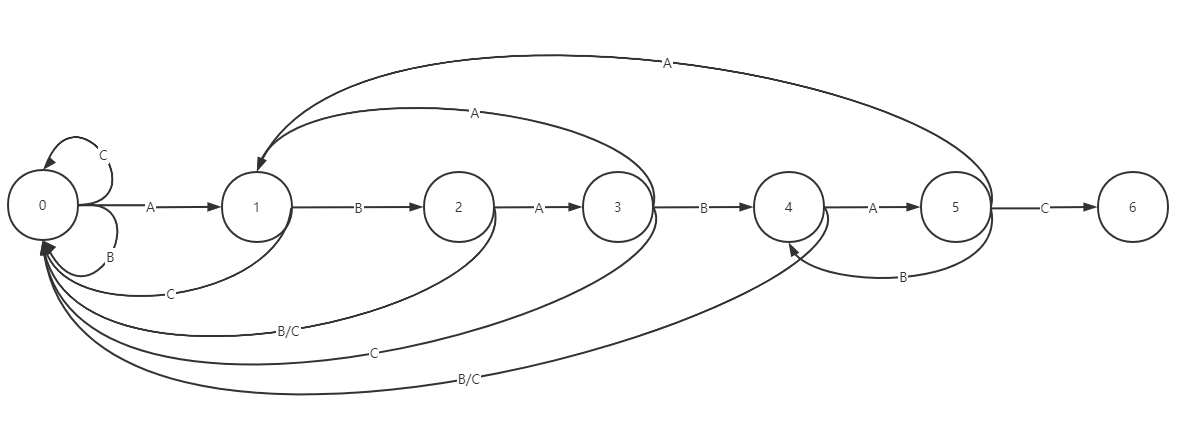
当推入字符C时匹配行进到下一步即 6 ,至此结束 当推入字符A时不匹配,掐头将剩下的字串BABAA推入自动机行进至 1; 当推入字符B时不匹配,掐头将剩下的字串BABAB推入自动机行进至 4
根据最终步骤画出的自动机,由此得到如下表:
| j | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| A | 1 | 1 | 3 | 1 | 5 | 1 |
| B | 0 | 2 | 0 | 4 | 0 | 4 |
| C | 0 | 0 | 0 | 0 | 0 | 6 |
2. 方法一: 直接计算
步骤如下:
j=0
| j | 0 |
|---|---|
| A | 1 |
| B | 0 |
| C | 0 |
只有当前字符是A才能往下一步走,所以只有(A,0)的值为1
j=1
| j | 0 | 1 |
|---|---|---|
| A | 1 | 1 |
| B | 0 | 2 |
| C | 0 | 0 |
有两种不完全匹配的情况AB和AC 已匹配模式串AA前缀有A
对于AB其后缀字串有B,它与已匹配字串的前缀子串最长匹配长度为0
对于AC其后缀字串有C,它与已匹配字串的前缀子串最长匹配长度为0
j=2
| j | 0 | 1 | 2 |
|---|---|---|---|
| A | 1 | 1 | 3 |
| B | 0 | 2 | 0 |
| C | 0 | 0 | 0 |
有两种不完全匹配的字符串ABB 和 ABC 已匹配模式串ABA前缀有AB A
对于ABB其后缀字串有BB,B。它们与已匹配字串的前缀子串最长匹配长度为0
对于ABC其后缀字串由BC,C。它们与已匹配字串的前缀子串最长匹配长度为0
j=3
| j | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| A | 1 | 1 | 3 | 1 |
| B | 0 | 2 | 0 | 4 |
| C | 0 | 0 | 0 | 0 |
有两种不完全匹配的字符串ABAA,ABAC
已匹配模式串ABAB前缀有ABA,AB,A
对于ABAA其后缀字串有BAA,AA,A,它们与已匹配字串的前缀子串最长匹配长度为1
对于ABAC其后缀字串由BAC,AC,C,它们与已匹配字串的前缀子串最长的匹配长度为0
j=4
| j | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| A | 1 | 1 | 3 | 1 | 5 |
| B | 0 | 2 | 0 | 4 | 0 |
| C | 0 | 0 | 0 | 0 | 0 |
有两种不完全匹配情况ABABB和ABABC 已匹配模式串ABABA前缀有ABAB, ABA, AB, A 对于ABABB其后缀有BABB, ABB, BB, B,它们与已匹配字串的前缀子串最长匹配长度为0 对于ABABC其后缀有BABC, ABC, BC, C,它们与已匹配字串的前缀子串最长匹配长度为0
j=5
| j | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| A | 1 | 1 | 3 | 1 | 5 | 1 |
| B | 0 | 2 | 0 | 4 | 0 | 4 |
| C | 0 | 0 | 0 | 0 | 0 | 6 |
有两种不完全匹配的情况ABABAA和ABABAB 已匹配模式串ABABAC前缀有ABABA, ABAB, ABA, AB, A
对于ABABAA其后缀字串有BABAA, ABAA, BAA, AA, A,它们与已匹配字串的前缀子串最长匹配长度为1
对于ABABAB其后缀字串由BABAB, ABAB, BAB, AB, B,它们与已匹配字串的前缀子串最长匹配长度为4
3. 方法二: 根据j-1 的情况推导当前 j 的情况
j=0
| j= | 0 |
|---|---|
| A | 1 |
| B | 0 |
| C | 0 |
j=1
| j= | 0 | 1 |
|---|---|---|
| A | 1 | 1 |
| B | 0 | 2 |
| C | 0 | 0 |
掐头去尾没有字符,故非匹配字符状态重复上一个状态即j=0
j=2
| j | 0 | 1 | 2 |
|---|---|---|---|
| A | 1 | 1 | 3 |
| B | 0 | 2 | 0 |
| C | 0 | 0 | 0 |
模式字串ABA掐头去尾得到B,无法对齐任何一位,故回到状态j=0
j=3
| j | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| A | 1 | 1 | 3 | 1 |
| B | 0 | 2 | 0 | 4 |
| C | 0 | 0 | 0 | 0 |
模式字串ABAB掐头去尾得到BA 无法对齐,故回到状态j=0
j=4
| j | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| A | 1 | 1 | 3 | 1 | 5 |
| B | 0 | 2 | 0 | 4 | 0 |
| C | 0 | 0 | 0 | 0 | 0 |
模式字串ABABA掐头去尾得到BAB 无法对齐,故回到状态j=0
j=5
| j | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| A | 1 | 1 | 3 | 1 | 5 | 1 |
| B | 0 | 2 | 0 | 4 | 0 | 4 |
| C | 0 | 0 | 0 | 0 | 0 | 6 |
模式字串ABABAC,掐头去尾得到BABA,错位对齐长度最大为 3 即
| B | A | B | A | |||
|---|---|---|---|---|---|---|
| A | B | A | B | A | C |
故回到状态j=3
4. 总结:
DFA自动机的构造过程不是特别困难,刚开始接触的时候可能理解起来有些吃力,但是多看几遍就释然了。 其实后两种计算方式都是自动机构造过程的某种延伸,只是它们比较容易用计算机实现出来而已。