1.背景
在常用的公开环境中,我们可能想说一些不想公开的悄悄话,这时候可能需要将悄悄话进行加密然后发送给对方。
这时候我们可以使用一种大家都知道的加密方式,并配置一个只有沟通双方知道的加密密钥。
这里加密方只需要提供待加密的数据和加密密钥,最后就会得到一串加密数据。解密方只需要拿到加密的数据然后使用加密密钥就能将数据解出来
过程如下:

这时候我们会发现,加密数据和加密密钥都需要通过一定的方法告诉解密方,如果有人在中间横插一杠偷偷拿到密钥怎么办?又或者是解密方拿着密钥冒充原始加密方怎么办?有没有一种方式可以不公开自己的加密密钥又能使得解密方能够解密呢?
当然有啦,公开密钥加密(也叫非对称加密)就是解决这些问题的。前面的加密方式称之为对称加密(即双方用一样的密钥,既能做加密方也能做解密方),参考对称加密
与之相对应的就是非对称加密,就是双方拿的密钥不同,加解密角色也不同。密钥分为两种,私钥和公钥。顾名思义私钥就是自己私藏的密钥,只用来解密用的;公钥就是可以公开的密钥,用来加密数据。当然反过来也是可以的,即用私钥加密数据,使用公钥解开。参考公开密钥加密
2.用法
2.1 生成密钥
首先得生成密钥,即公钥和私钥。通过openssl工具我们很容易实现
1
2
| openssl genrsa -out private_key.pem 2048
openssl rsa -in private_key.pem -pubout -out public_key.pem
|
2.1 加密和解密
这时候就可以使用公钥加密数据,然后使用私钥进行解密了
1
| echo 'hello world!' | openssl rsautl -encrypt -inkey public_key.pem -pubin -out encrypt_data.bin
|
我们这里把"hello world!“这条消息使用公钥加密一下,然后保存到encrypt_data.bin文件中,再使用私钥解密该文件
1
| openssl rsautl -decrypt -inkey private_key.pem -in encrypt_data.bin
|
得到的结果:
hello world!
签名和校验
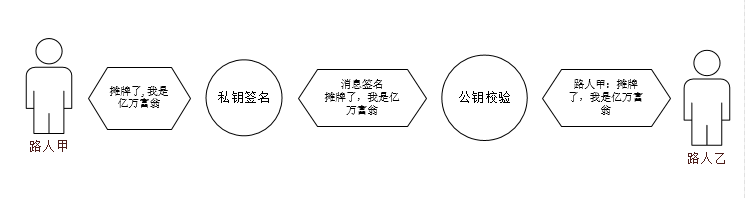
有时候我们并不需要将数据全部加密,因为这样效率有点低。例如两个人沟通其实并不需要多私密,只需要确定这句话是对方说的,且没有第三个人做了添油加醋即可。这样就可以不用带“翻译”,省去中间解密翻译的过程。
例如路人甲可以使用私钥对发的消息进行签名表明这条消息确实是他发的,然后把消息和消息签名一并告诉路人乙。路人乙拿到消息和消息签名,使用公钥校验一下这条消息的签名,确认无误后则相信路人甲确实发过这条消息。

3.原理
计算机算法的终点其实就是数学。当我第一次翻开《算法导论》这本书的时候,我翻开前几页我就看不下去了,因为我对数学并不感冒。上来就做数学公式的推导,本想着后面可能会讲到算法之类的,但是翻完后发现还是在做数学公式推导和证明。至此我坚信计算机算法都是数学在计算机领域的特定实现
公开密钥加密(非对称加密)的数学理论基础就是质数分解
加密就是:c(m) = m ^ e mod n
解密就是:m(c) = c ^ d mod n
这个过程中的公钥就是(n, e), 私钥就是(n, d)
n, e, d的计算过程如下:
选择两个不同的质数p和q。
一般选择比较大的增加暴力破解的难度,一般为512bit、1024bit或2048bit。为了方便计算,这里选择两个比较小的p=61, q=53
计算 n = p * q, 即n=3233
计算 l = lcm(p -1, q - 1), lcm为求最小公倍数, l= lcm(60, 52) = 780
确定 e 的值,这里取e = 17。其必须满足两个条件:
- 1 < e < l, 即 1 < e < 780
- e 和 l互为质数,即它们两最大公约数为1
计算 d 的值,d = 413。其也必须满足两个条件:
- 1 < d < l, 即 1 < e < 780
- e * d mod l = 1, 即 (17 * 413) mode 780 = 1
结果就是私钥为(n=3233, d=413),公钥为(n=3233, e=17)
我们使用这对密钥来尝试一下加解密数据, 例如我们需要加密的数据m=65:
加密后得到的数据为c = 65 ^ 17 mod 3233 = 2790
将密文c = 2790解密后, m = 2790 ^ 413 mod 3233 = 65
公式的证明过程可以参考引用里面的链接1
4.实现
涉及到加解密的实现那当然还得是openssl啦
rsa加解密入口在源码文件 apps/rsautl.c中:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| // openssl
switch (rsa_mode) {
case RSA_VERIFY:
rsa_outlen = RSA_public_decrypt(rsa_inlen, rsa_in, rsa_out, rsa, pad);
break;
case RSA_SIGN:
rsa_outlen =
RSA_private_encrypt(rsa_inlen, rsa_in, rsa_out, rsa, pad);
break;
case RSA_ENCRYPT:
rsa_outlen = RSA_public_encrypt(rsa_inlen, rsa_in, rsa_out, rsa, pad);
break;
case RSA_DECRYPT:
rsa_outlen =
RSA_private_decrypt(rsa_inlen, rsa_in, rsa_out, rsa, pad);
break;
}
|
分别是RSA校验,签名,加密,解密。签名校验原理上和加解密一致,只是使用的密钥不一样,所以我们只需要看加密和解密函数即可
参数默认情况的情况下,RSA_public_encrypt方式调用的是rsa_ossl_public_encrypt接口,实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| static int rsa_ossl_public_encrypt(int flen, const unsigned char *from,
unsigned char *to, RSA *rsa, int padding)
{
// 检查公钥的n值
if (BN_num_bits(rsa->n) > OPENSSL_RSA_MAX_MODULUS_BITS) {
RSAerr(RSA_F_RSA_OSSL_PUBLIC_ENCRYPT, RSA_R_MODULUS_TOO_LARGE);
return -1;
}
// 检查公钥的e值
if (BN_ucmp(rsa->n, rsa->e) <= 0) {
RSAerr(RSA_F_RSA_OSSL_PUBLIC_ENCRYPT, RSA_R_BAD_E_VALUE);
return -1;
}
/* for large moduli, enforce exponent limit */
if (BN_num_bits(rsa->n) > OPENSSL_RSA_SMALL_MODULUS_BITS) {
if (BN_num_bits(rsa->e) > OPENSSL_RSA_MAX_PUBEXP_BITS) {
RSAerr(RSA_F_RSA_OSSL_PUBLIC_ENCRYPT, RSA_R_BAD_E_VALUE);
return -1;
}
}
// ... 省略
// 对需要加密的内容进行填充,使其和密钥长度一致,方便加密
switch (padding) {
case RSA_PKCS1_PADDING:
i = RSA_padding_add_PKCS1_type_2(buf, num, from, flen);
break;
case RSA_PKCS1_OAEP_PADDING:
i = RSA_padding_add_PKCS1_OAEP(buf, num, from, flen, NULL, 0);
break;
case RSA_SSLV23_PADDING:
i = RSA_padding_add_SSLv23(buf, num, from, flen);
break;
case RSA_NO_PADDING:
i = RSA_padding_add_none(buf, num, from, flen);
break;
default:
RSAerr(RSA_F_RSA_OSSL_PUBLIC_ENCRYPT, RSA_R_UNKNOWN_PADDING_TYPE);
goto err;
}
// ... 省略
// 将填充好的二进制数据转换成大整数(big number)
if (BN_bin2bn(buf, num, f) == NULL)
goto err;
// ... 省略
// 计算密文, 加密方式:c(m) = m ^ e mod n
if (!rsa->meth->bn_mod_exp(ret, f, rsa->e, rsa->n, ctx,
rsa->_method_mod_n))
goto err;
// ... 省略
}
|
可以发现数据在进行加密的过程进行了填充,是因为:
- 解决数据不足一定长度的问题
RSA加密算法的核心是对明文进行幂运算,而每次幂运算的结果都只能是小于模数N的整数。因此,在明文长度小于N时,需要进行填充以保证明文长度满足加密要求。
- 防止明文被猜测或者攻击
由于RSA加密算法是公开的,攻击者可以通过分析加密结果来推断出明文信息。为了防止这种情况的发生,必须在加密前对明文进行填充,增加其复杂度,使得攻击者无法轻易地破解加密结果。
- 避免加密前后数据的长度不一致
在RSA加密过程中,如果明文没有进行填充,则加密后密文的长度通常会比明文短,这就会导致在传输过程中出现数据长度不一致的问题。为了避免这种情况的发生,需要对明文进行填充,以保证加密前后数据长度一致。
填充算法的实现可以参考RFC的文档,即引用链接3
再来看看解密函数RSA_private_decrypt, 即rsa_ossl_private_decrypt, 实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| static int rsa_ossl_private_decrypt(int flen, const unsigned char *from,
unsigned char *to, RSA *rsa, int padding)
{
// ... 省略
/* make data into a big number */
if (BN_bin2bn(from, (int)flen, f) == NULL)
goto err;
if (BN_ucmp(f, rsa->n) >= 0) {
RSAerr(RSA_F_RSA_OSSL_PRIVATE_DECRYPT,
RSA_R_DATA_TOO_LARGE_FOR_MODULUS);
goto err;
}
//...省略
// 解密数据,m(c) = c ^ d mod n
if (!rsa->meth->bn_mod_exp(ret, f, d, rsa->n, ctx,
rsa->_method_mod_n)) {
BN_free(d);
goto err;
}
// ... 省略
// 将解密后的大整数转换成字节形式
j = BN_bn2binpad(ret, buf, num);
// 检查填充及去除填充
switch (padding) {
case RSA_PKCS1_PADDING:
r = RSA_padding_check_PKCS1_type_2(to, num, buf, j, num);
break;
case RSA_PKCS1_OAEP_PADDING:
r = RSA_padding_check_PKCS1_OAEP(to, num, buf, j, num, NULL, 0);
break;
case RSA_SSLV23_PADDING:
r = RSA_padding_check_SSLv23(to, num, buf, j, num);
break;
case RSA_NO_PADDING:
memcpy(to, buf, (r = j));
break;
default:
RSAerr(RSA_F_RSA_OSSL_PRIVATE_DECRYPT, RSA_R_UNKNOWN_PADDING_TYPE);
goto err;
}
//... 省略
}
|
解密的过程其实和加密的过程是反过来的,只是使用的密钥及公式不同
5.引用
1.RSA
2.图文解释非对称加密
3.公开密钥加密表示实现